Программа ЭкзамL Предмет
Математика Тема: треугольники
Основные соотношения в треугольнике
Неравенство
треугольника: a + b > c; a + c > b; b + c > a
Сумма углов: a + b + g = 1800
Против большей стороны лежит больший угол, и обратно, против большего угла лежит большая сторона.
Против равных сторон лежат равные углы, и обратно, против равных углов лежат равные стороны.
 Средняя
линия
Средняя
линия
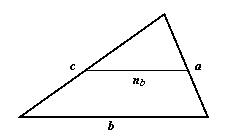
Средняя линия – отрезок,
соединяющий середины двух сторон треугольника.
·
Средняя линия
параллельна третьей стороне и равна её половине: ![]()
· Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.
 Медиана
Медиана
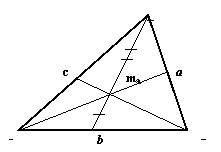
Медиана – отрезок,
соединяющий вершину треугольника с серединой противоположной стороны.
· Медианы треугольника точкой их пересечения делятся в отношении 2:1 (считая от вершины треугольника).
· Медиана делит треугольник на два треугольника с равными площадями.
![]()
Биссектриса
Биссектриса –
отрезок, выходящий из вершины треугольника и делящий угол пополам.
·
Биссектриса делит
противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
· Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
·
![]()
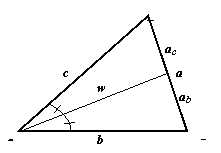
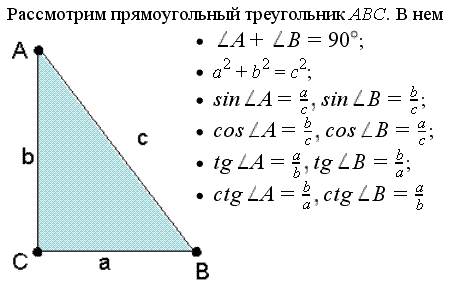
Прямоугольный треугольник
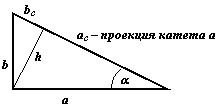
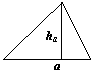
Теорема Пифагора: ![]() Площадь:
Площадь: ![]()
Тригонометрические соотношения: ![]()
Центр описанной окружности лежит на середине гипотенузы.
Радиусы окружностей:
![]()
Высота, опущенная на гипотенузу: 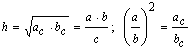
Катеты: ![]()
Равнобедренный треугольник
треугольник, у которого две стороны равны.
|
|
Углы, при основании треугольника, равны Высота, проведенная из вершины, является биссектрисой и медианой. |
Равносторонний треугольник
треугольник, у которого все стороны равны.
Все углы равны 600.
Каждая из высот является одновременно биссектрисой и медианой.
Центры описанной и вписанной окружностей совпадают.
Радиусы окружностей:
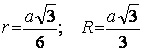
Площадь 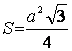
Площадь треугольника
![]()
![]()
![]()
![]()
![]()

Решение прямоугольных треугольников
Решение произвольных треугольников

Задачи
[1]. В треугольнике АВС
проведена медиана АМ. Найдите площадь треугольника АВС![]()
Ответ: 21
[2]. Основанием
пирамиды FABC является треугольник АВС, …. Отрезки АМ и AL являются
соответственно высотами треугольников AFВ и AFС.
Найдите объем пирамиды. Ответ в виде 137/27
Ответ: 128/41
[3]. Найдите радиус
окружности, вписанной в треугольник МРК 
Ответ: 24
[4]. Найдите сторону
ВC треугольника ВСD,![]()
Ответ: 16
[5]. Дан
прямоугольный треугольник АВС с прямым углом С. Через центр О вписанной в
треугольник окружности проведен луч ВО, пересекающий
катет АС в точке М. Найдите гипотенузу треугольника АВС.![]()
Ответ: 24
[6]. Площадь
треугольника АВС равна 20*Sqrt(3). Найдите АС, если
сторона АВ равна 8 и она больше половины стороны АС, а медиана ВМ равна 5.
Ответ: 14
[7]. Внешний угол при
основании равнобедренного треугольника равен 140°. Найдите угол между боковыми
сторонами этого треугольника.
1) 70°
+2) 100°
3) 40°
4) 80°
[8]. Сторона
равностороннего треугольника MLN равна
Ответ: 18
[9]. В равнобедренный
треугольник АВС с основанием ВС вписана окружность.
Она касается стороны АВ в точке М. Найдите радиус этой
окружности, если AM=10 и BM=15
Ответ: 7,5
[10]. Высоты
треугольника ABC пересекаются в точке Н, а медианы – в точке М. Точка K –
середина отрезка МН. Найдите площадь треугольника, если известно, что AB=6,
CH=3, <BAC=45° (< символ угла) Ответ в виде 78/34
Ответ: 45/8
[11]. В треугольнике
ABC угол C равен 90°, AB=5, cosA=0,8. Найдите BC
Ответ: 3
[12]. «Площадь
прямоугольного треугольника равна 27 см2. Длина одного
катета a на 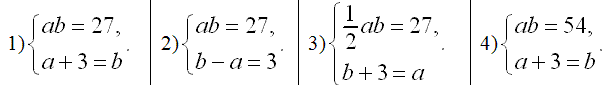
Ответ: 3
[13]. В треугольнике
ABC дано: AB = BC, AC = 10, высота CH равна 5. Найдите синус
угла ACB.
Ответ: 0,5
[14]. Найдите площадь
треугольника, изображенного на рисунке. Ответ запишите в виде число*sqrt(число )/ число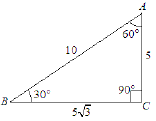
Ответ: 25*sqrt(3)/2
[15]. Острые углы прямоугольного
треугольника равны 24° и 66°. Найдите угол между высотой и медианой,
проведенными из вершины прямого угла. Ответ дайте в градусах.
Ответ: 42
[16]. В треугольнике
ABC AD - биссектриса, угол C равен 41°, угол CAD
равен 43° . Найдите угол B. Ответ
дайте в градусах.
Ответ: 53
[17]. На клетчатой
бумаге с клетками размером 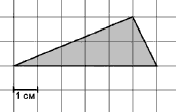
Ответ: 6
[18]. Найдите площадь
треугольника, вершины которого имеют координаты (1; 7), (7; 7), (6; 9).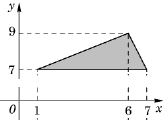
Ответ: 6
[19]. Треугольник ABC
вписан в окружность с центром O . Найдите угол BOC , если угол BAC равен 32°
Ответ: 64
[20]. В треугольнике
ABC угол C равен 90°, AB = 5, cosA = 0,8. Найдите BC.
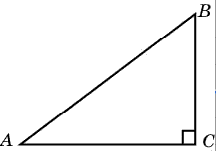
Ответ: 3
[21]. В треугольнике
ABC угол C равен 90°, AB = 10, BC = 8. Найдите cosA.
Ответ: 0.6
[22]. В треугольнике
ABC угол C равен 90°, AB =
Ответ: 0.75
[23]. В треугольнике
ABC угол C равен 90°, AB =
Ответ: 0.8
[24]. В треугольнике
ABC угол C равен 90°, AB = 15, BC = 9. Найдите косинус внешнего угла при
вершине A.
Ответ: -0.8
[25]. В треугольнике
ABC угол C равен 90°, tgA = 4/3, BC = 8. Найдите AB.
Ответ: 10
[26]. В треугольнике
ABC угол C равен 90°, cosA = 4/5, AC = 4. CH -
высота. Найдите AH.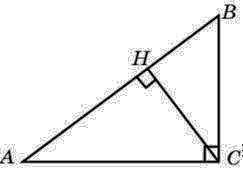
Ответ: 3.2
[27]. В
равнобедренном треугольнике ABC с основанием AC боковая сторона AB равна 25, а
высота, проведенная к основанию, равна 20. Найдите cosA.
Ответ: 0.6
[28]. В треугольнике
ABC AC = BC, AB = 23, cosA = 0.8. Найдите AC.
Ответ: 14.375
[29]. В треугольнике
ABC AC = BC = 5, AB = 4. Найдите cosA.
Ответ: 0.4
[30]. Найдите
гипотенузу прямоугольного треугольника, если стороны квадратных клеток равны 1.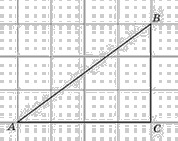
Ответ: 5
[31]. В треугольнике
ABC AC = BC, AB = 5, высота AH равна 4. Найдите cosA.
Ответ: 0.8
[32]. В тупоугольном
треугольнике ABC AB = BC, AC = 25, CH - высота, AH = 15. Найдите синус угла
ACB.
Ответ: 0.8
[33]. В треугольнике
ABC AC = BC = 20, AB = 36. Найдите cosA.
Ответ: 0.9
[34]. В треугольнике
ABC AC = BC, AB = 10, высота AH равна 1. Найдите sinA.
Ответ: 0.1
[35]. В треугольнике
ABC угол C равен 90°, CH - высота, BC = 25, BH = 20. Найдите sinA.
Ответ: 0.8
[36]. В треугольнике
ABC AC = BC = 12, sinB = 3/5. Найдите AB.
Ответ: 19.2
[37]. В треугольнике
ABC AC = BC = 8, AB = 4. Найдите cosA.
Ответ: 0.25
[38]. В треугольнике
ABC угол C равен 90°, синус внешнего угла при вершине A равен 0.5, AB = 8.
Найдите BC.
Ответ: 4
[39]. Найдите площадь
треугольника, изображенного на клетчатой бумаге с размером клетки 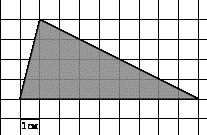
Ответ: 18
[40]. Найдите площадь
треугольника, изображенного на клетчатой бумаге с размером клетки 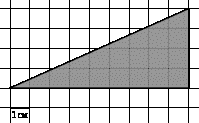
Ответ: 18
[41]. Найдите площадь
треугольника, изображенного на клетчатой бумаге с размером клетки 
Ответ: 9
[42]. Найдите площадь
треугольника, изображенного на рисунке.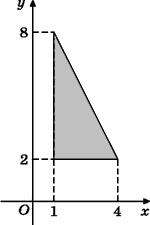
Ответ: 9
[43]. Найдите площадь
треугольника, изображенного на клетчатой бумаге с размером клетки 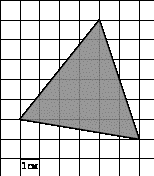
Ответ: 17
[44]. Найдите площадь
треугольника, изображенного на рисунке.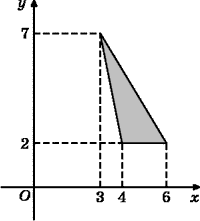
Ответ: 5
[45]. Найдите площадь
треугольника, изображенного на рисунке.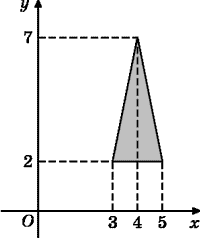
Ответ: 5
[46]. Основанием
прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 4.
Площадь ее поверхности равна 132. Найдите высоту призмы.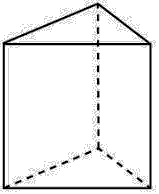
Ответ: 10
[47]. Отметьте верные
утверждения
1) Если две стороны
одного треугольника соответственно равны двум сторонам другого треугольника, то
такие треугольники равны.
+2)
Если расстояние от центра окружности до прямой больше радиуса, то эти прямая и
окружность не имеют общих точек.
+3) Диагонали
параллелограмма в точке пересечения делятся пополам.
4) Площадь трапеции
равна произведению основания трапеции на высоту.
5) Сумма углов
тупоугольного треугольника больше 180°.
[48]. Отметьте верные утверждения
1) Диагонали параллелограмма
равны.
+2) Два различных
диаметра окружности пересекаются в точке, являющейся центром этой окружности.
+3) Сумма углов
трапеции равна 360° .
4) Площадь
прямоугольного треугольника равна произведению катетов.
+5) Синус острого
угла прямоугольного треугольника равен отношению противолежащего катета к
гипотенузе.